看了别人的代码直接看不懂，加了printf才明白
他的博客链接：https://www.cnblogs.com/crackpotisback/p/3964249.html
定理：若图G中含有Euler通路，则称图G为半欧拉图。若一个图是欧拉图或者是半欧拉图，则称该图是可以遍历的。

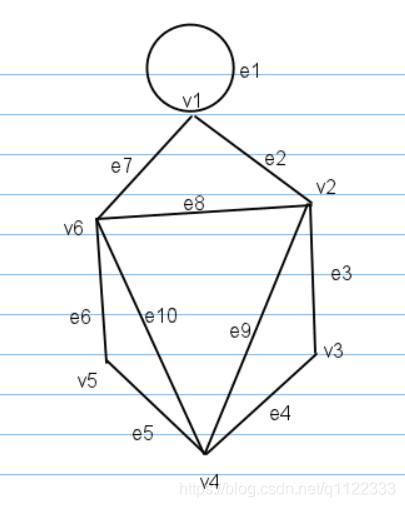
如果所有的顶点的度都为偶数，那么就可以随便指定一个点做欧拉环游
如果顶点的度为奇数的个数为2，那么欧拉通路的起点或者顶点应该为这两个顶点。
从V1开始，第一次的dfs为 v1->v2->v3->v4>v2->v6->v1，并将这些顶点依次入栈，并且每次删掉边，出栈的时候判断下该顶点还有没有其它路径，如果有的话，就要以它为顶点再找个闭迹，然后把闭迹上的点依次入栈。
v6出栈时，发现e6,e10还没被删掉，对它进行一次dfs，每次dfs就是在剩下的边找一条闭迹 v6->v4->v5->v6,并把这些顶点一次入栈。
出栈的顶点就构成了一条欧拉迹。

/*
六个顶点10条边 
6 10
1 1 
1 2 
1 6
2 3 
2 4 
2 6
3 4
4 5 
4 6
5 6
*/ 
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <climits>
#include <vector>
#include <queue>
#include <cstdlib>
#include <string>
#include <set>
#include <stack>
#define LL long long
#define pii pair<int,int>
#define INF 0x3f3f3f3f
using namespace std;
const int maxn = 1000;
bool e[maxn][maxn];
int n,m;
stack<int>stk;
void dfs(int u){
    stk.push(u);
    cout<<u<<"入栈"<<endl;
    for(int i = 1; i <= n; i++){
        if(e[u][i]){
            e[u][i] = false;
            e[i][u] = false;
            cout<<u<<" "<<i<<"的边删除掉"<<endl;
            cout<<"dfs "<<i<<endl;
            dfs(i);
            cout<<"dfs "<<i<<" 结束"<<endl; 
            break;
        }
    }
}
void Fleury(int x){
    while(!stk.empty()) stk.pop();
    stk.push(x);
    cout<<x<<"起点入栈"<<endl; 
    int i;
    while(!stk.empty()){
        int u = stk.top();
        stk.pop();
        cout<<u<<"出栈"<<endl; 
        for(i = 1; i <= n; i++)
            if(e[u][i]) break;
           if(i <= n) 
           {    
               cout<<"找到边"<<u<<"，并dfs它 "<<u<<endl;
            dfs(u); 
           } 
           else
           {
            printf("欧拉路径：%d \n",u);
        } 
        cout<<"一次循环结束"<<endl; 
    }
    puts("");
}
int main() {
    int u,v,cnt,degree,st;
    while(~scanf("%d %d",&n,&m)){
        memset(e,false,sizeof(e));
        for(int i = 0; i < m; i++){
            scanf("%d %d",&u,&v);
            e[u][v] = e[v][u] = true;
        }
        cnt = 0;
        st = 1;
        for(int i = 1; i <= n; i++){
            for(int j = 1,degree = 0; j <= n; j++)
            {    
                if(e[i][j]) degree++;
            } 
            if(degree&1)
            {
                st = i;
                cnt++;
            }
        }
        if(cnt == 2 || !cnt) Fleury(st);
        else puts("No Euler path");
    }
    return 0;
}